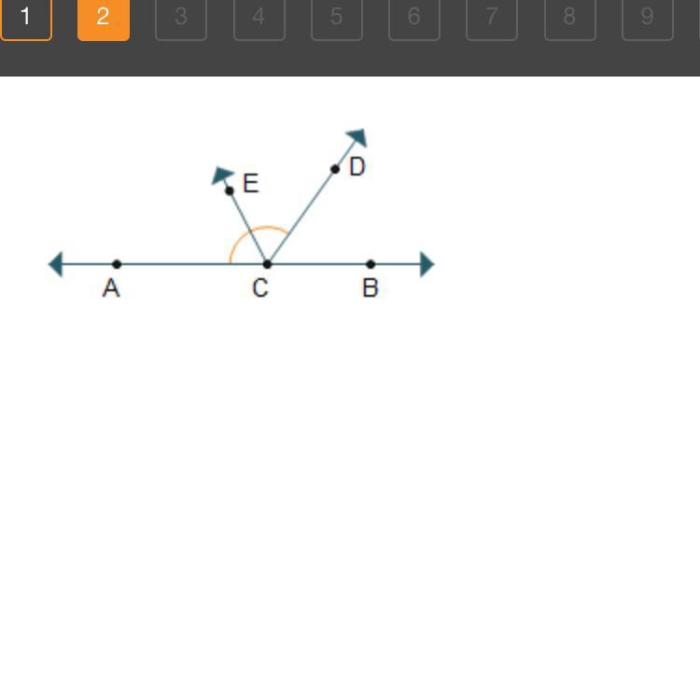
Ray ce is the angle bisector of acd – Ray CE is the angle bisector of angle ACD. This means that ray CE divides angle ACD into two congruent angles, ∠ACE and ∠ECD. Angle bisectors are important in geometry because they can be used to construct congruent angles, perpendicular lines, and bisecting segments.
In this article, we will discuss the definition of an angle bisector, the properties of angle bisectors, and the constructions related to angle bisectors. We will also explore the applications of angle bisectors in geometry.
Angle Bisectors: Properties and Applications: Ray Ce Is The Angle Bisector Of Acd
In geometry, an angle bisector is a ray or line that divides an angle into two congruent parts. It plays a crucial role in various geometric constructions and applications.
Definition of Angle Bisector
An angle bisector is a ray or line that originates from the vertex of an angle and bisects it into two equal angles. It is commonly denoted by the symbol ‘∠’.
For example, if we have an angle ∠ABC, the angle bisector would be a ray or line that originates from point B and divides ∠ABC into two congruent angles, ∠ABF and ∠CBF.
Ray CE as the Angle Bisector of Angle ACD
In the given diagram, ray CE is the angle bisector of angle ACD. It divides ∠ACD into two congruent angles, ∠ACE and ∠ECD.
Properties of Angle Bisectors:
- An angle bisector is perpendicular to the segment connecting the two sides of the angle it bisects.
- It divides the angle into two congruent parts.
- Angle bisectors can be used to construct congruent angles.
Properties of Angle Bisectors
Angle bisectors possess several important properties:
- Perpendicularity:An angle bisector is always perpendicular to the line segment connecting the two sides of the angle it bisects.
- Congruency:An angle bisector divides an angle into two congruent parts. This means that the two angles formed by the angle bisector and the sides of the angle are equal in measure.
- Construction of Congruent Angles:Angle bisectors can be used to construct congruent angles. By constructing an angle bisector for a given angle, we can create two new angles that are congruent to each other.
Constructions Related to Angle Bisectors, Ray ce is the angle bisector of acd
Constructing an angle bisector using a compass and straightedge involves the following steps:
- Draw the angle you want to bisect.
- Place the compass point on the vertex of the angle.
- Adjust the compass to a radius greater than half the length of the sides of the angle.
- Draw two arcs that intersect outside the angle.
- Draw a line connecting the two points of intersection. This line is the angle bisector.
Applications of Angle Bisectors in Geometry
Angle bisectors have numerous applications in geometry, including:
- Finding the Center of a Circle:The angle bisectors of the interior angles of a triangle intersect at a single point, which is the center of the circle that circumscribes the triangle.
- Constructing Perpendicular Lines:Angle bisectors can be used to construct perpendicular lines to a given line segment. By constructing an angle bisector for an angle formed by two intersecting lines, we can create a line perpendicular to one of the lines.
- Bisecting Segments:Angle bisectors can also be used to bisect line segments. By constructing an angle bisector for an angle formed by two intersecting lines, we can create a line that bisects the segment formed by the intersection of the lines.
Helpful Answers
What is an angle bisector?
An angle bisector is a ray that divides an angle into two congruent angles.
What are the properties of angle bisectors?
Angle bisectors are perpendicular to the sides of the angle they bisect. They also divide the angle into two congruent angles.
How can you construct an angle bisector?
You can construct an angle bisector using a compass and straightedge. First, draw an arc that intersects both sides of the angle. Then, draw another arc that intersects the first arc and the vertex of the angle. The line that connects the two points of intersection is the angle bisector.